这项研究缘起于如下问题：

如果你总共拥有5000点副属性，并且你可以自由地分配它们。那么，为了使你的DPS最大化，你将如何分配?

A.全部分给爆击

B.按照某种比例分配给爆击和溅射

C.按照某种比例分配给爆击、溅射和精通

D.按照某种比例分配给所有的5种副属性

E.其他

我对这个问题非常感兴趣，正确的答案究竟是什么?为什么?

我希望能够以某种较为科学的方法来尝试性地回应这一问题。

前 言

本文的研究问题是:当副属性总值为N时，如何分配各项副属性，使得其对DPS的提升最大?

正文分为3个部分，如果将此研究比喻为对Y = F(X)的研究，那么，

第一部分，探讨了定义域X的问题。

第二部分，估算了一些参数，建构了F(X)。

第三部分，讨论了有限的结论，即使得F(X)取最大值时，X在副属性上的最优分布。

说 明：

1. 本研究聚焦于WOD6.23版本，主要在地狱火堡垒(普通、英雄、史诗)所提供的装备等级范围(690~740)内进行讨论。

2. 本研究以“装备4T18套装”“狩猎刺激天赋”“孤狼天赋”为讨论基础，对于不具备4T18套装特效以及非孤狼天赋的情况没有进行讨论。

3. 研究情景围绕团队副本Raid，对于PVP方面的副属性没有讨论。

装等、属性与定义域

通过查阅WOWDB数据库中的部分装备信息，经由Excel表整理和计算，得出一些较为通用的信息。

这些信息为本研究的定义域划分提供了部分数据上的基础。(如果您已熟知这部分信息，请直接从第二部分开始阅览)

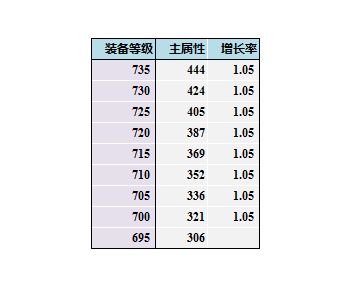
1.一件装备(非饰品)为你提供多少主属性和副属性，和装备等级直接相关。如下图所示，装等为695到735的头部锁甲，其主属性值分别从306增加到444。

2.一件装备(非饰品)上的“主属性”与“副属性之和”的比例为3：4。1、2两条联系起来看，意味着一旦你的装等确定了，你所能获得的副属性总和也确定了。无论对某一职业来说，哪些属性是优势属性，哪些是劣势属性，这些暴雪都不管，给了你这么多装等，总值就确定了。剩下的问题就是选择和搭配了。

3.在690至740这个装等范围内，装等每提高5%，主副属性就增长5%。(例如，700装等的头部锁甲比695装等的头部锁甲所拥有的敏捷值多5%;735装等的头部锁甲比730装等的头部锁甲所拥有的敏捷值多5%)这意味着装等越高，主副属性的总值增长的就越快，同样相差15个装等，725装等距离740装等的属性，其绝对数值差异，要略高于700装等相距715装等间的差距。

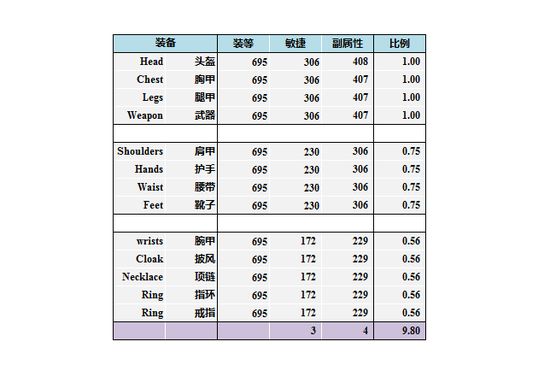
4.装等完全相同的装备，其装备上的主副属性值与装备的部位有关。(具体的比例关系如下图所示)头、胸、腿和武器这4件装备提供的属性值最多且相等。肩、手、腰、脚4个部位的装备提供的属性为同装等头甲的75%。披风、护腕、项链、指环提供的属性为同装等头甲的56%。若将各个部位的比例求和，得到的值为9.8。有了上述数据，我们可以在不计饰品的情况下，较为快速地估算出处于某一装等的100级猎人，从装备上获得的主属性和副属性和大致为多少。也正因如此，由于每位玩家不同部位的装等往往不一样，因而游戏插件中显示的平均装等就有“虚低”和“虚高”的可能。

5. 饰品并非像其他装备一样提供稳定的主副属性，而是有着相对多样的设计，因此不在本研究中重点讨论。但是，本研究的部分结论，或对于饰品的选择有一定的帮助。

6. 以上述数据为参考，若以装等为690~740作为本研究的研究范围，那么估算出的副属性总和接近于3815~6070的范围。考虑到附魔和饰品(常驻或触发)可能带来的副属性增益。因而，将本研究的定义域确定在副属性总值为4000~8000的范围内。事实上，6000+的副属性总值已经接近毕业水平，但是考虑到武器附魔和饰品使用或触发带来的短时间内的副属性增长，因而将研究的最高范围定在8000。

系数估算与公式构建

首先，我们需要从猎人技能伤害的一般公式开始思考。

zstotal大大在《急速集中学导论》中讨论相关副属性问题时，将其表述为：

DPS=总加成系数0•(基本伤害+AP*系数1)•(1+基础爆击率+爆击等级/系数2)•(1+基础急速率+急速等级/系数3)•(1+基础精通率+精通等级/系数4)•(基础命中率+命中等级/系数5)

llxibo大大在《SimulationCraft完全手册》中表述为：

r = DPS(crit, haste,mastery, hit, expertise, dps-weapon, speed-weapon,...)

DeXter215大大在《猎人常用伤害技能说明》中的公式，可以概括为：

Damage = F(AP, Weapon)*F(Secondary Stats)

而在本研究中，F(AP，Weapon)即，有关武器伤害和主属性的部分，暂不讨论。那么剩下的，就是我们关注的：

Y = F(Secondary Stats)

这里的Y，记为：副属性综合收益系数。这个函数构成了我们研究问题的核心，它表述为：

Y = (1+爆击率*爆击系数)*(1+溅射率*溅射系数)*(1+精通率*精通系数)*(1+全能率*全能系数)*(1+急速率*急速系数)

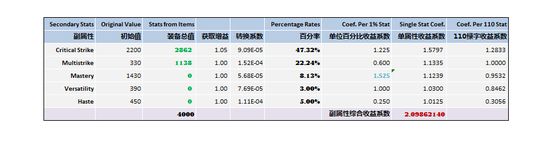
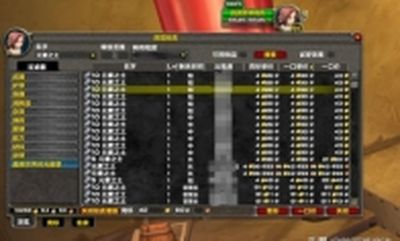
副属性综合收益函数表

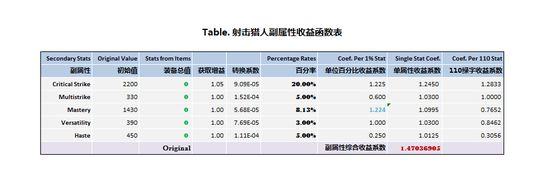
上表，就是截至目前为止，我设定的副属性收益函数。

本节余下的所有部分，就是阐明这张表中的数据和公式是如何得出来的。

下节的任务是使用这一工具来回答研究问题——“使得DPS最大化的N点副属性总值的分配问题”。

关于此表的部分说明

1. 第一列.副属性

陈列了猎人的5项副属性，依次为爆击、溅射、精通、全能、急速。

2. 第二列.初始值

以绿字的形式表述了100级猎人拥有的副属性初始值。此处所指的初始值包括两部分，裸体属性和团队Buff。合剂、药剂、食物、强化符文等物品未列入讨论中。

3. 第三列.装备总值

相当于函数中的X部分，是下一节计算时，填入不同数值使用的。此时各项副属性的数值相当于0。

4. 第四列.获取增益

作为一个系数，对于射击猎人来说，主要指“致命射击”这一被动天赋。拥有额外5%的爆击获取率，因而其系数为1.05。对于其他副属性来说，全是1。

5. 第五列.转换系数

表中为科学记数法，因为数值都比较小，写成分数形式依次是1/11000，1/6600，1/17600，1/13000，1/9000。这些系数就是方便将绿字形式的副属性表述为百分率形式的副属性而使用的。其意义就相当于110点爆击等于1%爆击率，因而用110去乘以这个系数就等于1%了(后面的同理)。

6. 第六列，百分率

就是以百分率的形式来呈现各项副属性的多少。在此表中，该列的百分比会根据初始数值和列3中填入的数值自动计算出角色某一状态下的副属性百分比。这一列的数值是此函数表的重要参数。

7. 第七列.副属性的单位百分比受益系数

该系数描述“每1%的某种副属性将转化为多少总DPS的增长”。该列同样是此函数表的重要参数。

8. 第八列.单属性收益系数

陈列了各项副属性在被赋予某一特定值时，对总DPS的增益。绝大多数情况下，该列的数据是根据“百分率”和“单位百分比收益系数”计算出来的，计算公式就是我们熟知的(1+副属性百分率*单位百分比收益系数)。但是，精通属性是个例外，关于这个例外我们会在下文精通系数部分详细阐述。

9. 第九列.110绿字属性收益系数

如果我们估算出了单位百分比收益系数，我们就自然地得知了每110绿字的受益系数。这一系数，方便我们从绝对数值方面进行比较各项副属性(毕竟不同的副属性，其1%所需的绿字各不相同，因而比较不同的1%副属性未必有可比性)。

10. 底行.副属性综合收益系数

将5个“单属性收益系数”相乘，得到该值。它是我们投入、分配、重铸(选择宝石和附魔)各项副属性时，最应关注的系数。它集中体现了当前属性值下，所有副属性综合起来对DPS的提升力度。本研究精确到小数点后8位数，其中的原因之一是该精度下，对于任意1点副属性的增减都有足够的敏感度，从而方便我们进行比较。上表的数值，可以默认为裸体且团队Buff齐全状态下的数值。是我们比较的起点，也是最低值。

溅射、全能和急速系数的估算

由于副属性强化技能的机制和范围不同，使得我们在计算“每1%某种副属性对于总DPS的提升”这一问题时，面临的复杂性也不尽相同。

溅射 Multistrike(0.600)

就射击猎人而言，1)所有的技能都可以从溅射属性中获得收益;2)所有技能从溅射属性中获得的收益率都是稳定的。

每1%的溅射属性，可以提升我们0.6%的伤害。因而，溅射属性的单位百分比系数为0.60。这一系数可以从溅射的作用方式直接推到出来，此处不再赘言。

全能 Versatility(1.000)

和溅射属性相同，射击猎人的所有技能可以从全能属性中获得稳定的收益。1%全能提升1%伤害，因而这个系数为1.000。

急速 Haste(0.250)

急速这一属性对于射击猎人的作用方式比较复杂。

1)急速可以提高集中值的被动回复速度(可惜太微弱了)

2)急速与其他触发性Buff的加成关系是乘法，而非加法，因而在一定程度上提升了急速属性的收益

3)在4T18套装特效下，只有自动射击和稳固射击(在达到急速上限以前)能够从急速属性中获益，这个获益率可以认为每1%急速提升自动射击和稳固射击1%的伤害。

4)自动射击和稳固射击在射击猎人的伤害构成中，一般为20%左右。而其他的技能(奇美拉射击、瞄准射击、夺命射击)的急速收益为0。

尽管急速对射击猎人的作用方式相比溅射和全能复杂，但是，由于第1条(急速作用于被动集中回复的能力太弱)和第4条(约80%伤害的技能无法从急速中受益)，急速对射击猎人的伤害加成能力依旧很弱。此处，将急速的单位百分比受益系数定位0.250。尽管0.250的系数是粗略估算出来的，但是它并不影响我们后续对属性分配的影响，因为在本研究所讨论的范围内，任何情况下DPS理想最大值的分配方案中，急速属性都为0。Z大若干年前的那句话“猎人不爱急速”如今依旧适用。对于猎人来说，急速并不重要，重要的是如何不要急速。

爆击、精通系数的估算

构建这个函数最难的地方，在于如何估算“爆击和精通”对于DPS伤害加成的系数。

1. 在最一般的情况下(所有技能都能爆击，技能爆击伤害为原伤害的2倍)，1%爆击属性对于猎人的提升也是1%，即，爆击系数是1.00。

2. 射击猎人的被动技能“强化瞄准射击”(爆击的瞄准射击回复20点集中)使得1%爆击对于猎人的伤害提升大于1.00。因而，这个由“强化瞄准射击”带来的提升需要估算，并纳入新的系数中。

3. 射击猎人的精通机制为“每m%精通提升伤害m%，且提升m%爆击伤害”。复杂点在于精通的后半部分，提升m%爆击伤害。这部分被提升的爆击伤害是计入爆击属性的收益，还是计入精通属性的收益?这个问题必须规划清楚，以便在构建函数的过程中，既不忽视副属性对DPS的提升方式，又不重复计算。

两种等价的表述形式

假设(一)

如果将爆击伤害提升计入爆击属性里，精通属性则只能保留前一部分的效果。

在这种条件下，设：爆击率为c%，精通率为m%

则：

爆击属性的收益系数：1+c%*(1+2m%)------------------(1)

精通属性的收益系数：(1+m%)------------------------(2)

假设(二)

如果将爆击伤害提升计入精通属性里。设：爆击率为c%，精通率为m%，非爆击伤害为d

求：精通收益公式和爆击收益公式。

爆击属性的收益系数：(1+c%)-------------------------------------------------(3)

精通属性的收益系数：[1+ (2c%(m%)^2+3c%m%+m%)/(1+c%)]----------------(4)

精通率为0%时，DPS(0%) = d(1-c%)+2d*c%

精通率为m%时，DPS(m%) = d(1-c%)(1+m%)+2d(1+m%)*c%*(1+m%)

精通属性的收益系数= [DPS(m%)- DPS(0%)] / DPS(0%)

化简后，即得到上式。

爆击与精通的纠缠关系

将“爆击属性的收益系数”乘以“精通属性的收益系数”，我们发现两种假设情况下，这一乘积是相同的：

式(1)*式(2)=式(3)*式(4)=1+c%+m%+3c%m%+2c%(m%)^2

上式表明了爆击属性与精通属性是如何“纠缠在一起”“共同作用于”DPS的提升。因为无论如何，无法把上式转化成“一个只含有c%的式子”与“一个只含有m%的式子”的乘积。因而，爆击和精通的关系更为密切，不像急速、溅射和全能，后三者可以较为独立地作用于DPS，但是爆击和精通则不行。

对于爆击和精通来说，如果没有其他的影响，我们完全可以直接将上述公式带入副属性综合收益函数中，至此我们建构函数的工作就将结束，剩下的就是如何求解了。但是，就爆击而言，需要将“强化瞄准射击”带来的增益纳入进来，而由于实战中“狙击训练”难以保持100%的覆盖率，因而，我打算给精通的收益在上述理想公式上乘以一个0.9的系数。意味着90%覆盖率下的精通收益，以此，纳入到最终的函数式中来。因此，我们还必须选择一种将爆击和精通分开的方式，而不能直接选择“它们的共同作用公式”。显然，假设(2)的情况更符合我们的需求。

至此，精通的收益系数为：1+0.9*[ 2c%(m%)^2+3c%m%+m%]/(1+c%)

经过一些模型假设和计算(在此过程中我使用了块秒伤的理论参与构建假设的模型，此贴中，我将省略对这一部分的详细阐述)，我估算出的爆击收益系数约在1.20至1.25之间，我取了中间值1.225纳入到最终的函数中。

至此，必要的公式和参数全部构建完成，于是我们有了下面的公式：

射击猎人副属性综合收益= (1+c%*1.225)* {1+0.9*[ 2c%(m%)^2+3c%m%+m%]/(1+c%)}*(1+溅射率*0.6)*(1+全能率*1.0)*(1+急速率*0.25)

根据这一公式，编写了计算使用的Excel表格。

结 论

前面两部分的工作，一方面，我们确定了副属性总值处于4000-8000范围的定义域。另一方面，通过一些数理模型和估算部分重要参数，我们搭建了一个副属性综合收益的函数。

我不清楚这是一个怎样的函数，也不清楚这是一个几元几次的函数，更谈不上去求解这个函数。但是，为了能够对研究问题提供一些有参考性的数据，我还是用一些特殊的方式来求解当副属性总值分别为4000，5000，6000，7000和8000时，副属性的最优分布。

计算的方式是利用Excel表，手动计算。这种方式既不便利，也不繁琐，只是有些机械而已。

简言之，就是填入一些数字，然后改变其中的某些数字，再与原来的结果进行比较，如果大于原来的则保留该结果并继续变换，直到发现最优分布为止。好在，由于急速和全能对射击猎人的加成力度太小，以至于在研究范围内，最优分布中它们的取值都为0，因此，我们的最优分布事实上就有研究5个变量变成研究3个变量，这极大地减少了人工运算的时间。进行一次总值确定的人工计算大约需要15~20分钟，总值越大，计算时间相对越长。

计算的结果如下:

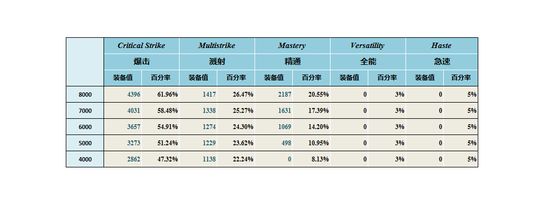
这张表只采集了玩家们更关心的“副属性绿字数值”与该数值下包括初始属性的“面板百分率”。具体的其他数据，例如不同取值下副属性的“单位百分比收益系数”、“单属性收益系数”以及“110绿字收益系数”在附件的表格中可以查看得到。

副属性收益简评

爆击

综合来看，爆击依旧是猎人最优秀的副属性。“入场”最早，在考察范围内贯穿始终都是占比最高的副属性。爆击属性最大化的原则几乎可以通吃WOD版本的整个时期。

溅射

作为暴雪在WOD版本力推的新属性，该属性收益稳定且收益率尚可。对于所有职业来说，110点溅射属性的收益率都不会小于1.00。

然而，就射击猎人而言，在副属性总值较低的情况下(副属性总之约为4500或以下)，溅射牢牢占据了第二优属性的位置。但是，随着副属性总值的提升，较高的爆击率进一步实现了精通属性对DPS提升的潜在能力，从而使得精通的受益系数急剧提升，随之而来的就是在高属性总值阶段，溅射率在最优分布中的提升力度非常缓慢。

数据显示，副属性总值从4000提升到8000时，最优分布下的溅射率仅从22.24%提升至26.47%，在副属性总值4000点的巨额增幅中，最优分布下的溅射属性仅增长了279点(1417-1138)，约等于项链、披风、戒指附魔一套。

这一结果对目前我们对副属性的普遍认识或许是有一定冲击作用的。6.0和6.1时代的所谓“爆击，溅射”是比较符合当时的实际的，但是在6.23版本下，或许这一认识需要扭转。

同时，溅射数据要求我们重新审查和评估带溅射的饰品，尤其是触发或主动使用提升溅射的饰品。他们的收益率究竟如何，是否接近最优分布?因为，溅射充斥着各个装等阶段的装备，且它以及“堆得很高”。24%左右的溅射率是在6.1版本中就可以实现的，那么，一些诸如“试图将溅射率堆至40%再配上溅射饰品”的想法和做法或许需要调整了。在版本末期，最优分布给我们提出的问题是，如何防止溅射偏高。

精通

爆击率的提升，释放了精通对DPS的提升潜力，使得精通在版本末期开始逐渐超越溅射，称为第二优属性。

在上面的函数中，考虑到“狙击训练”Buff在Raid中难以100%覆盖，因而取了90%覆盖率的系数。随着对战斗流程的熟练，实战中，如果狙击训练Buff的覆盖率在90%以上，那么精通属性将比表格中列出的数值更具优势，会相对更早、更快地超越溅射属性。

精通的数据同样对当前的一种普遍想法“主爆击、副溅射、精通随缘”提出了挑战。版本末期，暴雪给我们的精通装并不充足，尤其是饰品。之所以计算到8000点副属性总值，就是想查看在副属性触发情况下，副属性的最优分布。很遗憾，数据并不支持溅射类触发饰品。爆击和精通反而更具优势，但是，原有的对仔细瞄准下部分爆击率对瞄准射击和稳固射击不再提升的担心依旧有一定的道理。我现在反倒希望能有一款触发精通的饰品了，起码对武器附魔来说，或许精通附魔会得到更广的使用。简言之，版本末期，精通成为更值得我们去“堆”的第二副属性了。

全能&急速

一对难兄难弟。很遗憾，在我们所考察的范围内，这两项副属性在最优分布中没有“入场”的几率。是射击猎人需要极力减少的副属性。

全能对PVE环境下的输出职业提升力度，稳坐全联盟倒数第一。我在想暴雪是否应该将全能放入PVE防御职业属性与PVP通用属性的情境下设计装备。

急速，依旧是Z大多年前的那句话——猎人不爱急速。

装备选择方面的建议

如果用最简洁的话来概括6.23阶段射击猎人的装备配置，请接近下属分布：

爆击率54%，溅射率24%，精通率14%

触发类的属性，触发精通最优，溅射最次。触发爆击，涉及到对仔细瞄准阶段爆击收益折扣的计算，本文没有精确地计算。弱忽略这部分折扣，爆击触发也是略优于溅射，单如果这部分折扣较大，则可能低于溅射。

需要说明的是，由于66点溅射带来1%溅射率的提升，而176点精通才带来1%精通的提升，因而不要被面板上较高的溅射率数字所迷惑。副属性总值到了某一阶段，请酌情降低溅射，提升精通。

一些闲谈与讨论

如果说有什么早已存在的东西触发了我对副属性最优分布的兴趣，那么可以追溯到初中数学课上关于(a+b)等于定值时，(1+a)*(1+b)的最大值问题。暴雪设计了5种副属性，在某一装等水平下，角色获得的副属性总值又是一定的，于是就有了最优分布的问题了。

关于研究的局限与不足

首先，研究者本身水平有限。我的数学、计算机、英语水平都非常有限，因而，研究此类问题时大体上只能在“加减乘除四则混合运算”和“初等函数”的层面上进行思考。

其次，一些系数的估算有待进一步推敲。由于爆击-精通系数收实战中的影响较大，不同的狙击训练Buff覆盖率、不同的技能使用比例都会影响这两项副属性的系数。因而，我就只能采取一些模型来估算。原则上，我是希望这些模型能够更加接近实际。但距离实际情况的距离究竟有多远，我也无法说清。因而，系数偏差有可能影响到最终的结果。

一些展望

IIxibo大大在《SimulationCraft完全手册》谈到了公式建模与仿真建模各自的特点。我本人十分认同其中的观点，并且我认为随着游戏设计的不断复杂，对于某些问题的回答，或许需要两种建模之间更为紧密的结合。

就本研究而论，显然属于公式建模的体系内。一方面，在一些参数的估算方面，如果能够有仿真建模提供的一些数据支持的话，参数估算的精度会更高。另一方面，如果完善后的公式——副属性收益函数是较为有效和可信的，那么通过设计一些插件来自动计算最优分布的结果，取代手动计算，会使得我们更为方面地求得某些最优分布解。

附录：4000-8000副属性总值下的最优分布

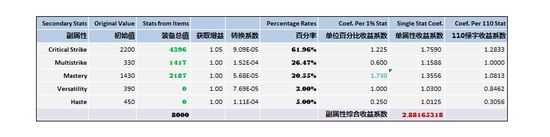
最优分布(N=8000)

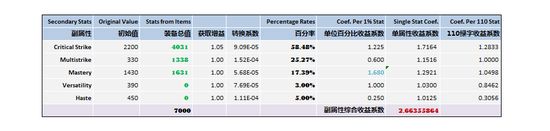
最优分布(N=7000)

最优分布(N=6000)

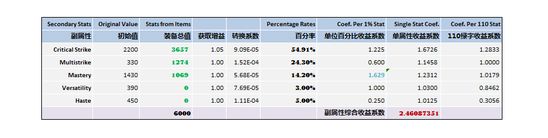
最优分布(N=5000)

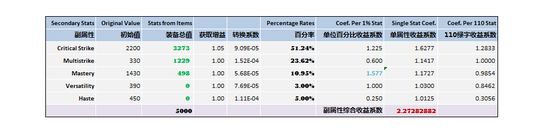
最优分布(N=4000)